安価なオシロスコープで1MHzを1kHzで振幅変調した波形が見られないのはどういうことか考えてみた。
(音声)信号の1kHzの正弦波の一周期に搬送波の1MHzは1000周期分が入る。これをデジタル化するには二倍の2000ポイントより多くサンプルする必要がある。サンプリング周波数としては2MHzより高くなければならない。とはいえ、それは(永遠に)繰り返す波形をマクロ的に捉える場合。オシロスコープのように一瞬を捕まえて表示するのであれば、それが元の波形のように見えるにはその周波数の10倍とか20倍のレートでサンプリングしないとそれらしく見えないはず。仮に10倍だとしても、1MHzの信号をそれらしく見ようと思ったら10MHzのサンプリングレート(10MSa/s)が必要ということになる。
ADS1013Dのスペックではサンプリングレート(の上限)は1GSa/s。10MSa/sよりは遥かに高いのでこの点は問題ない。
ストレージ深度は240Kbitと記載されている(要するにメモリの量)。ADコンバータの精度は8bitなので、レコード長は30K(ポイント)ということかな?そうだとして、10MSa/sの30Kポイント分の時間は、(1/10E6)*30E3 = 0.003[s]、つまり、3ms。1kHzの1周期は1msだから3周期分。ADS1013Dは画面表示の前後数倍の長さを記録しているようなので、仮に1kHzの1周期を画面に表示させるには、実際には10周期分くらいのメモリが必要。10周期だと10msなので、メモリが足りないってことになす。それを避けるにはサンプリングレートを落とすしかない。
この関係は搬送波と信号波の相対的なものだから、搬送波の周波数を下げるか、信号波の周波数を上げればメモリに余裕が生まれる。
ということで実験。
まずは、搬送波1MHz、信号波100kHzで。
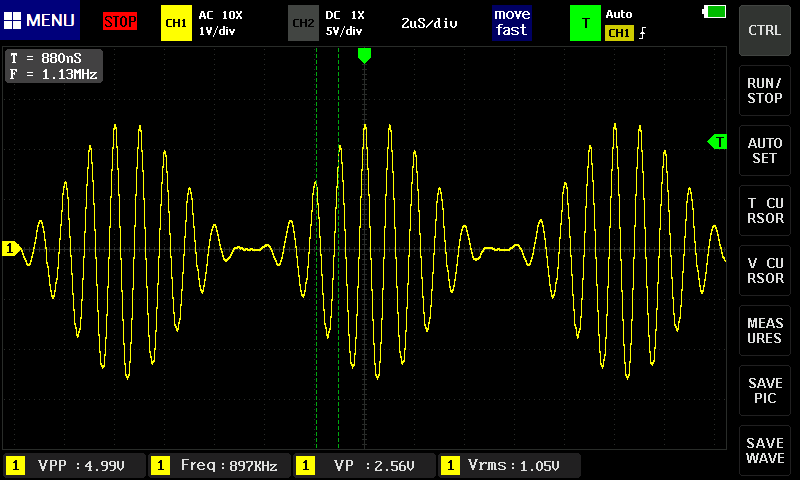
それらしく見える。
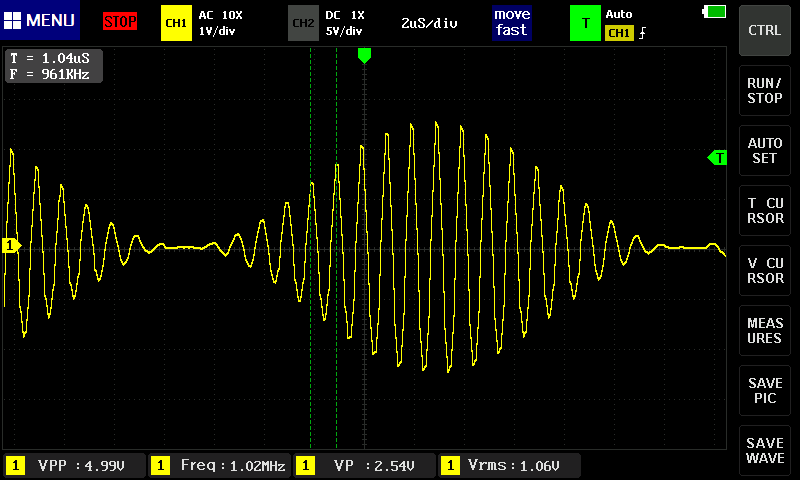
続いて、50kHz(搬送波は1MHzで固定)。
さらに下げて20kHz。画面から大きくはみ出すので、水平軸は伸ばす。
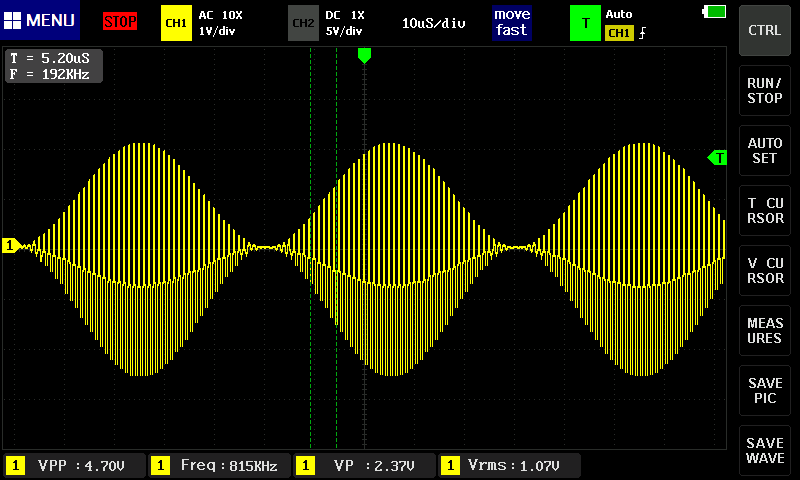
エイリアシングが見えてきた(という表現でいいのか?)。
10kHz。
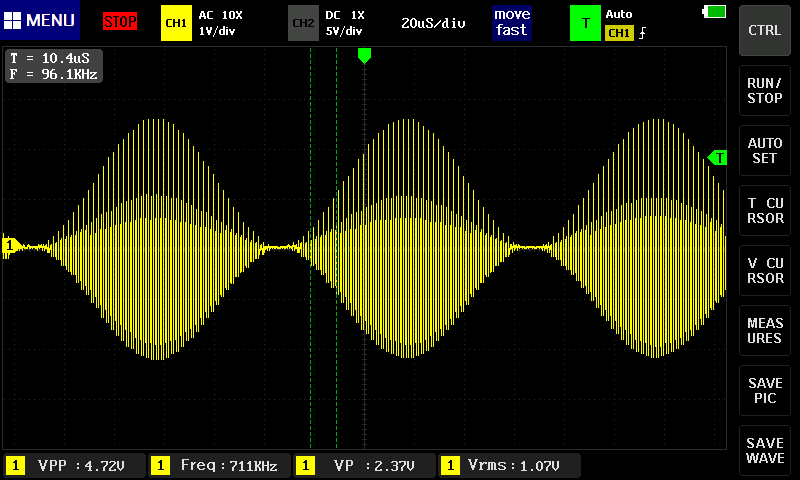
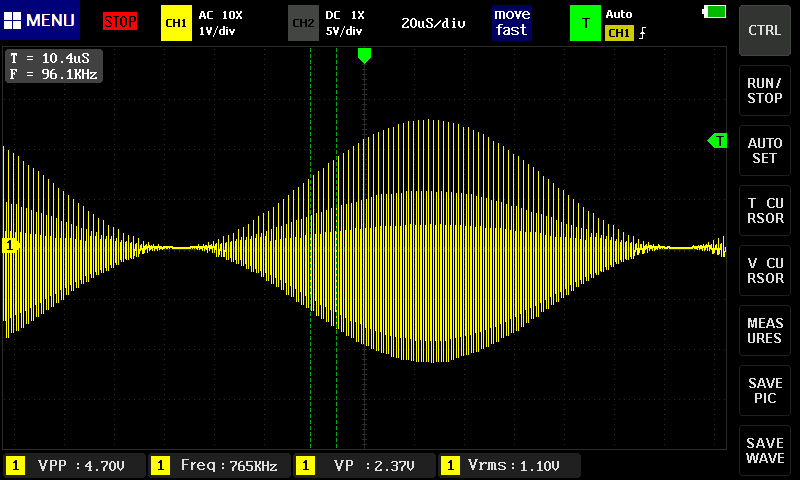
1kHz。
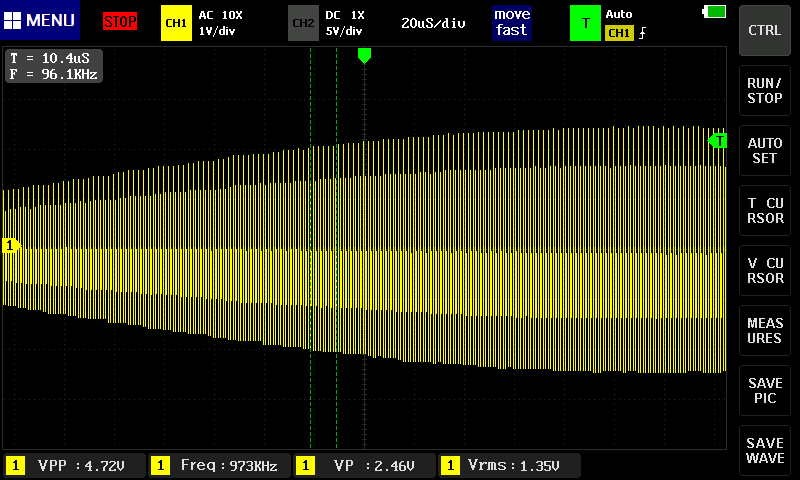
画面からのはみ出した大きいので時間軸を伸ばすと…
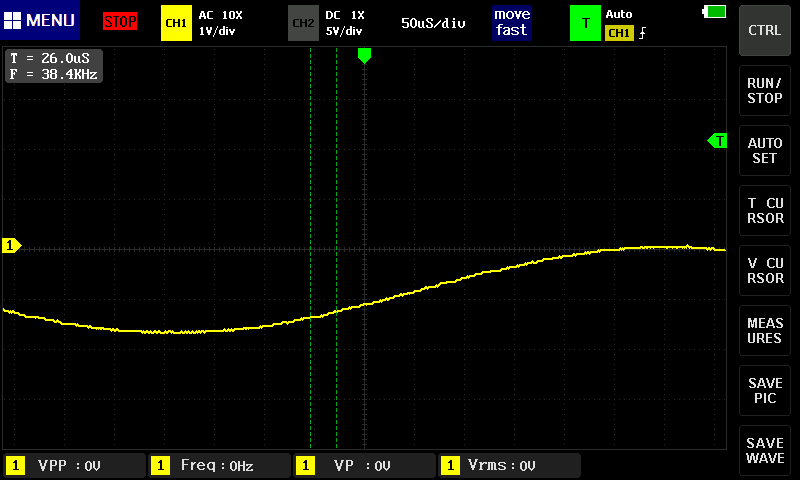
搬送波として見えなくなり、完全にエイリアシングの状態。
このことから、水平軸を遅くするとサンプリング周波数を下げていることがわかる。そうしないとメモリに収まらないのでしょうがない。
ゆっくりとした信号の観測の中で速い変化を見るのは無理だということ。デジタルオシロなので当たり前といえば当たり前。何が起きているかわかったのでスッキリした。これがわかっていれば、まぁ、安心して使えるかな。しかし、それにしてもメモリが少ないんだなぁ。単純にメモリの容量だけの話じゃなくて、容量を大きくするためには高速にアクセスできるメモリじゃなきゃダメだから高いんだろうな。
ちなみに、Micsig STO1104Cではメモリ長(レコード長)は28M(ポイント)なので、これくらいは余裕(4ch同時に使うとchあたりは7M)。
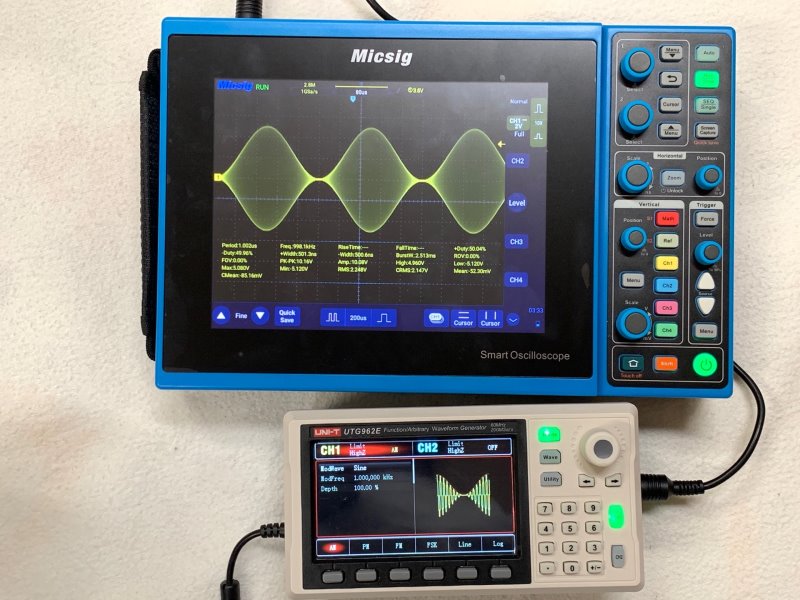
アナログオシロはメモリを使わないのでそもそもこのようなことは起きない。見方を変えると、ブラウン管がメモリ(昔の電子計算機ではブラウン管をメモリとして使ったものもあった)。


コメント