「Arduino、サーミスタ、温度計」という三題噺みたいな入門記事をよく見かけるけど、「うーん…」と思うものが多々。
サーミスタの抵抗値を求める
サーミスタは温度によって抵抗値が変わるデバイス。したがって、サーミスタの抵抗値を求めれば温度に変換できる。
電圧検出
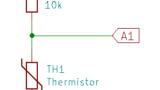
検出部の回路は、概ねこんな感じ。
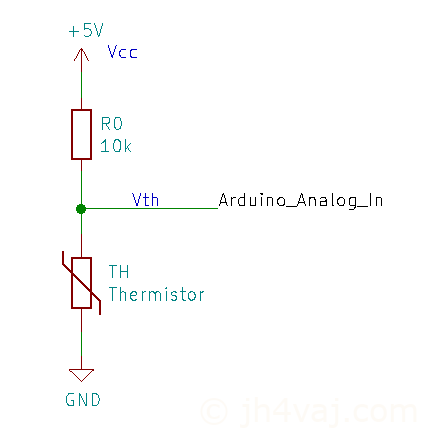
サーミスタの電圧(Vth)をArduinoで測って、基準抵抗(R0)との比でサーミスタの抵抗値を求める。アナログ入力の練習問題みたいなもの。抵抗とサーミスタが逆のパターンもあるけど、どっちにしても電源電圧を分圧したところを測るというものなので、本質的なところは同じ。なお、この回路は、ArduinoのVrefがVccであることが前提(Arduinoのデフォルト)。
電圧を計算して抵抗値を導き出す
上の図で、Vthを求めるにはこう。
\[ Vth=\frac{Vcc}{1024} \times X \]
ここで、\(X\)はArudinoで読み取った値、1024はArduinoのADコンバータの分解能(10ビット)。VccをADコンバータの分解能で割った値は、1ビットあたりの電圧。
例えば、読取り値\(X\)が600だと、こうなる。
\[ Vth=\frac{5}{1024} \times 600 \]
\[ =2.9297[V] \]
ここから、サーミスタの抵抗値(Rth)は次のように求められる(抵抗の比とそれぞれの電圧の比は等しいので)。
\[ Rth=\frac{Vth}{Vcc-Vth} \times R0 \]
\[ =\frac{2.9297}{5-2.9297} \times 10 \]
\[ =14.1511[kΩ] \]
サーミスタの抵抗値が求まったので、あとはこれを使って温度に変換すれば良い。
※上の値は、電圧を小数点以下四桁で丸めているのでその分の誤差がある。実際にはもっと細かい値まで計算しているので、誤差は小さい。
【追記】
当初、計算式を間違えていた。詳細はこちらの記事。本ページは修正済み。
【追記ここまで】
電圧を計算せずに抵抗値を導き出す
上のようなやり方で説明している記事を結構多く見かけるのだけど、「うーん…」と思う。それは、サーミスタの電圧(Vth)を求めていること。そんな必要はないんだけど。
知りたいのはサーミスタの抵抗値であって電圧ではない。抵抗値がわかればいいのでわざわざ電圧を求める必要はない。 ADコンバータがVref(=Vcc)のときの値(1024、ADコンバータの分解能と同じ値)と読取り値\(X\)をそのまま使っても抵抗値は求められる。
\[ Rth=\frac{X}{1024-X} \times R0 \]
\[ =\frac{600}{1024-600} \times 10 \]
\[ =14.1509[kΩ] \]
これでもちゃんとサーミスタの抵抗値は求まる。しかも、電圧を経由したりしないので計算もシンプル。単純な比の話であって、電圧は関係ない。
電圧測定の問題点
抵抗値を求めるのであれば、どっちでも問題ない(計算の手間は置いておくとして)。が、もし電圧を求めたいのなら問題がある。
5Vは本当に5Vか?
計算の根拠を電圧が5Vであると仮定しているので、その電圧の精度が測定結果に影響する。
例えば、Arduino Nanoの場合、電源周りの回路はこうなっている(公式の回路図から引用)。
まず、外部電源(VIN)。
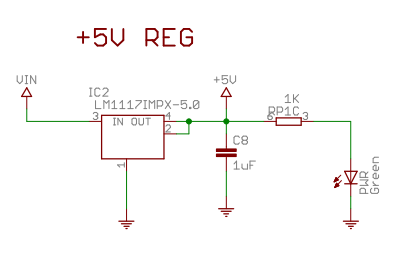
レギュレータ1117で5Vを作っているので、この精度次第。
続いて、USB給電の場合。
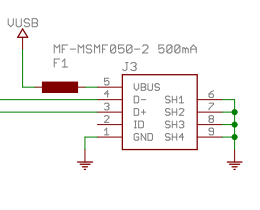
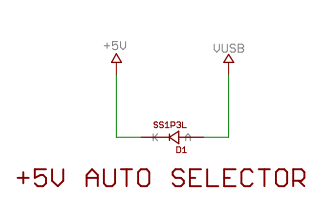
USB端子からの電源は、フューズ(ポリスイッチ)とSS1P3L(ショットキーバリアダイオード)経由で供給される。SS1P3LはのVfはデータシートによると0.35V。これは1Aの場合なので、Arduino Nanoで使う程度ならそこまで大きくはないだろう。0.2Vくらい?
また、そもそもUSBからの電源電圧が5Vかというと、結構怪しい。これが4.9Vだとして、SS1P3LのVfが0.2Vだと仮定すると、+5Vとして供給されるのは、実際は4.7Vということになる(ポリスイッチでもわずかに電圧降下があるけど、これは無視しておく)。
つまり、5Vだと思っていたものが4.7Vだったとしたら、6%の誤差を持っていることになる(ちなみに、手元のArduino Nanoを普段使っているデスクトップPCにつないでVINをデジタルテスタで測ったら4.5Vくらいだった)。
計算例
上の例(読取り値Xが600の場合)を使って計算してみる。
+5Vが本当に5Vであるなら、先に計算したように、Vthは2.9297V。
もし、+5Vが実は4.7Vであるなら、
\[ Vth=\frac{4.7}{1024} \times 600 \]
\[ =2.7539[V] \]
-0.1758Vの誤差が生じる(供給電圧に比例するので、-6%)。
念のため補足すると、抵抗値を計算するのであれば問題ない。上で書いたように、計算結果では電源電圧(ADコンバータのリファレンス電圧)に比例するところは消えるため。
まとめなど
サーミスタの抵抗値を求めるのに、わざわざ電圧を計算する必要はない。
基準抵抗との比が分かればよいだけなので、ArduinoのADコンバータの値をそのまま使えばOK。
求める抵抗値には電源電圧(ADコンバータの基準電圧)の絶対値は影響しない。基準抵抗の精度だけが影響する。
【メモ】
\[\frac{Vth}{Vcc} = \frac{Rth}{R0+Rth} \]
\[ Vth(R0+Rth) = Vcc \cdot Rth \]
\[ Vth \cdot R0 + Vth \cdot Rth = Vcc \cdot Rth \]
\[ Vth \cdot R0 = Vcc \cdot Rth – Vth \cdot Rth \]
\[ Rth(Vcc – Vth) = Vth \cdot R0 \]
\[ Rth = \frac{Vth }{Vcc – Vth} R0 \]
【追記】サーミスタは自己発熱する。サーミスタに流す電流を小さくしないと高めの温度を表示してしまう。



コメント