日本無線協会のWebサイトで解答が発表された。前日に発表されたQCQ企画のものと同じ(ま、当然だろうが)。ということで、法規 148点、無線工学 128点が確定。マークシートでのミスがなければだけど。
ここで誤答を振り返っておく。
法規
「エ」について、G1Bの主搬送波の変調の型式が「位置変調」になっているのが間違い。「位相」でなく「位置」という、誤記・誤字のようなところ。過去問でも何度か出てきたので知っているの引っかかってしまった。間違い探しの注意力を試される問題。
そうかぁ。簡素でなきゃいけないのかぁ。
そういえば、今回のB問題は、すべて「適合するものを1、適合しないものを2」という○×式だった。
無線工学
解き方:
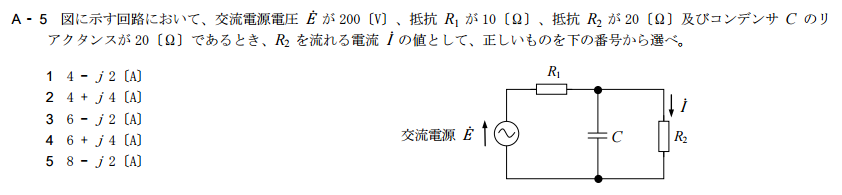
- まず、回路全体に流れる電流(\(=R_1\)を流れる電流)を求め、
- \(R_1\)にかかる電圧を算出し(オームの法則)、
- \(\dot{E}\)からその電圧を引くと残りが\(C\)および\(R_2\)に掛かる電圧なので、
- あとは、その電圧を\(R_2\)で割れば\(\dot{I}\)が求められる。
- そのために、最初に\(C\)と\(R_2\)の合成インピーダンスを求めるところから始める。
では、早速。最初にその\(C\)と\(R_2\)の合成インピーダンス(ここでは、\(\dot{Z_b}\)とする)を算出する。
$$\frac{1}{\dot{Z_b}}=\frac{1}{20}+\frac{1}{-j20}=(中略)=\frac{1+j}{20}$$
$$\dot{Z_b}=\frac{20}{1+j}=(中略)=10-j10\ [\Omega]$$
したがって、\(R_1\)を含めた回路全体のインピーダンス(\(\dot{Z_a}\)とする)は次のようになる。
$$\dot{Z_a}=20-j10\ [\Omega]$$
\(R_1\)を流れる電流(=回路全体の電流、ここでは、\(\dot{I_a}\)とする)を求める。
$$\dot{I_a}=\frac{\dot{E}}{\dot{Z_a}}=\frac{200}{20-j10}=(中略)=8+j4\ [A]$$
\(R_1\)の両端の電圧は、\(\dot{I_a}\cdot R_1=(8+j4)\times 10=80+j40\ [V]\)なので、\(C\)と\(R_2\)にかかる電圧(\(\dot{E_b}\)とする)は、全体の電圧からこの電圧を減じたもの。
$$\dot{E_b}=200-(80+j40)=120-j40\ [V]$$
したがって、\(R_2\)に流れる電流\(\dot{I}\)は、
$$\dot{I}=\frac{120-j40}{20}=6-j2\ [A]$$
となる。
で、間違ったのは、\(\dot{E_b}=200-(80+j40)=160-j40\)としてしまったこと。算数苦手…。結果、\(8-j2\)となってしまう。選択肢にこの値がなければ気がつくのに^^;
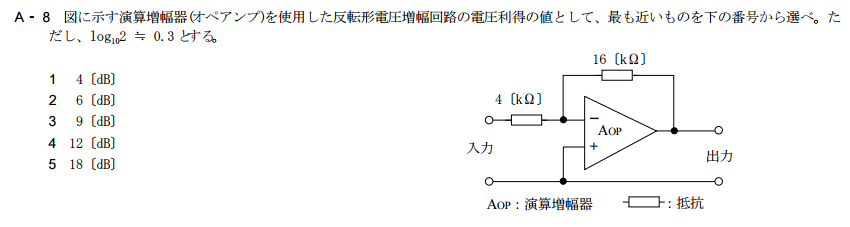
電圧利得なので、2倍にしなきゃけいけないのを忘れていた。
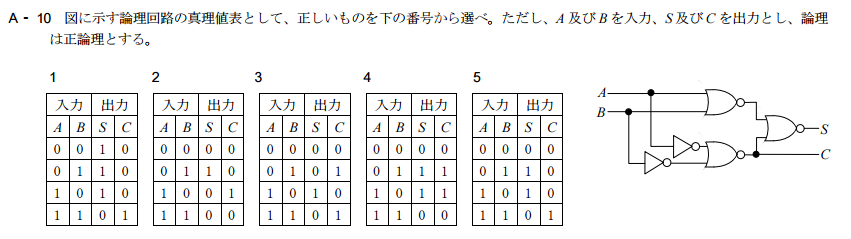
これに関しては、何をどう思ったのか、出力端子はSしか目に入っていなかった。そこだけ見ればXOR回路。Cもあるので、これは半加算器。
ご丁寧に出力端子にS(Sum)とC(Carry)とあるので、答えを書いてくれているようなものなのに…。悔しい、というか、情けなさすぎる。
コリニアアレーはもちろん知っているけど、なぜか興味を覚えないのでちゃんと調べたことがなかった。λ/4かλ/2かが問われているようなもので、λ/4に勝負をかけたら失敗だった^^;
「エ」はファラデーの法則。「オ」はレンツの法則。入れ替わっている。こういうのは覚えるのが苦手…。
以上、反省会終了。






コメント
A-5の問題の途中式
Ia˙=E˙Za˙=20020−j10=(中略)=8−j4 [A] とありますが、その下で正しい8+j4 [A]になっていますから直しておいた方が読んだ人を混乱させないと思います。
久々に複素数の式解きました。ありがとうございます。
本当ですね。ご指摘下さり、ありがとうございます。早速、修正しました。